
艺术风格转移的卷积神经网络
课程视频见:https://www.bilibili.com/video/av19891729/
总结
其实就像最基本的二分类问题一样,任何机器学习的问题的解决无非是这几个步骤,了解问题是什么,数据准备,然后选择解决问题的机器学习模型,然后训练模型,测试模型,周而复始,大功告成。
构建和训练模型的目的是“教会机器解决问题”,两大部分。一是“如何衡量学习效果”,也就是找到合适的损失函数来考核每一次训练的效果如何,二是“让机器不断进步”也就是找到合适的最优化方法最小化损失,使每一次的训练都能让机器“学”到东西。
按这个思路对今天的问题进行总结:
- 问题描述:图像风格转移,即让我们可以将任何给定图像的“画风”转移到另一个图像上面。
- 模型选择:16层卷积神经网络(CNN),VGG16。
- 损失函数:我们将使用我们选择的隐藏层的输出来分别计算样式和内容的损失函数。
- 优化方法:,类似于随机梯度下降法,即L-BFGS。
机器学习创作艺术,创作音乐,机器学习写作…….这类主题是最吸引我的,这些主题同样也是很难的。作为深度学习入门的部分,很多数学的,神经网络的东西这里就先浅尝辄止了,以后慢慢在做深入。
艺术风格转移
本文的程序是对这篇倍受欢迎的论文Gatys et al., 2015的python代码实现,它演示了如何使用神经网络将艺术风格从一个图像转移到另一个图像上(如下图)。并且作为这篇博客文章的补充。

依赖库
from __future__ import print_function
import time
from PIL import Image
import numpy as np
from keras import backend
from keras.models import Model
from keras.applications.vgg16 import VGG16 # CNN模型
from scipy.optimize import fmin_l_bfgs_b # 优化方法
from scipy.misc import imsave
数据准备
需要的输入数据分为内容图像(content image)和样式图像(style image),下面将对这两个图像进行加载和预处理。
图像导入
用PIL将图片导入并将大小一致设置为512×512
# 内容图像
height = 512
width = 512
content_image_path = 'images/hugo.jpg'
content_image = Image.open(content_image_path)
content_image = content_image.resize((height, width))
content_image
out[1]:

# 样式图像
style_image_path = 'images/styles/wave.jpg'
style_image = Image.open(style_image_path)
style_image = style_image.resize((height, width))
style_image
out[2]: 
图像预处理
然后,我们将这些图像转换成适合数值处理的形式。需要注意的是,我们添加了另一个维度(超越了经典高度*宽*RGB值三维),这样我们就可以将这两个图像的表示连接到一个公共的数据结构中。
content_array = np.asarray(content_image, dtype='float32')
content_array = np.expand_dims(content_array, axis=0)
print(content_array.shape)
style_array = np.asarray(style_image, dtype='float32')
style_array = np.expand_dims(style_array, axis=0)
print(style_array.shape)
out[3]:
(1, 512, 512, 3)
(1, 512, 512, 3)
在进一步进行之前,我们需要对输入数据进行按摩,以匹配所做的工作。Simonyan and Zisserman (2015)介绍了我们即将使用的VGG网络模型。
为此,我们需要执行两个转换:
- 从每个像素中减去平均RGB值(从谷歌搜索中可以很容易地得到)。
- 将多维数组的顺序从RGB转到BGR(在论文中使用的顺序)。
content_array[:, :, :, 0] -= 103.939
content_array[:, :, :, 1] -= 116.779
content_array[:, :, :, 2] -= 123.68
content_array = content_array[:, :, :, ::-1]
style_array[:, :, :, 0] -= 103.939
style_array[:, :, :, 1] -= 116.779
style_array[:, :, :, 2] -= 123.68
style_array = style_array[:, :, :, ::-1]
现在我们已经准备好使用这些数组来定义Keras后端中的变量。我们还引入了一个占位符变量来存储组合图像,它保留了内容图像的内容,同时包含了样式图像的样式。
content_image = backend.variable(content_array)
style_image = backend.variable(style_array)
combination_image = backend.placeholder((1, height, width, 3))
最后,我们将所有这些图像数据连接到一个单独的张量中,这个张量适合Keras的VGG16模型的处理。
input_tensor = backend.concatenate([content_image,
style_image,
combination_image], axis=0)
VGG模型
这里重用一个预先训练好的模型(VGG)来定义损失函数。Gatys et al. (2015)提出的核心思想是,对图像分类预先训练好的卷积神经网络(CNNs)已经知道如何编码图像的感性和语义信息。我们将遵循他们的想法,并使用由一个这样的模型提供的特性空间来独立地处理图像的内容和样式。
原始论文使用19层VGG网络模型从Simonyan和Zisserman(2015),而是我们要遵循Johnson et al .(2016)使用16层模型(VGG16)。在做出这个选择时没有显著的质量差异,我们在速度上略有增加。
此外,由于我们对分类问题不感兴趣,我们不需要全连接的层和最终的softmax分类器。我们只需要下面表格中绿色标记的部分。
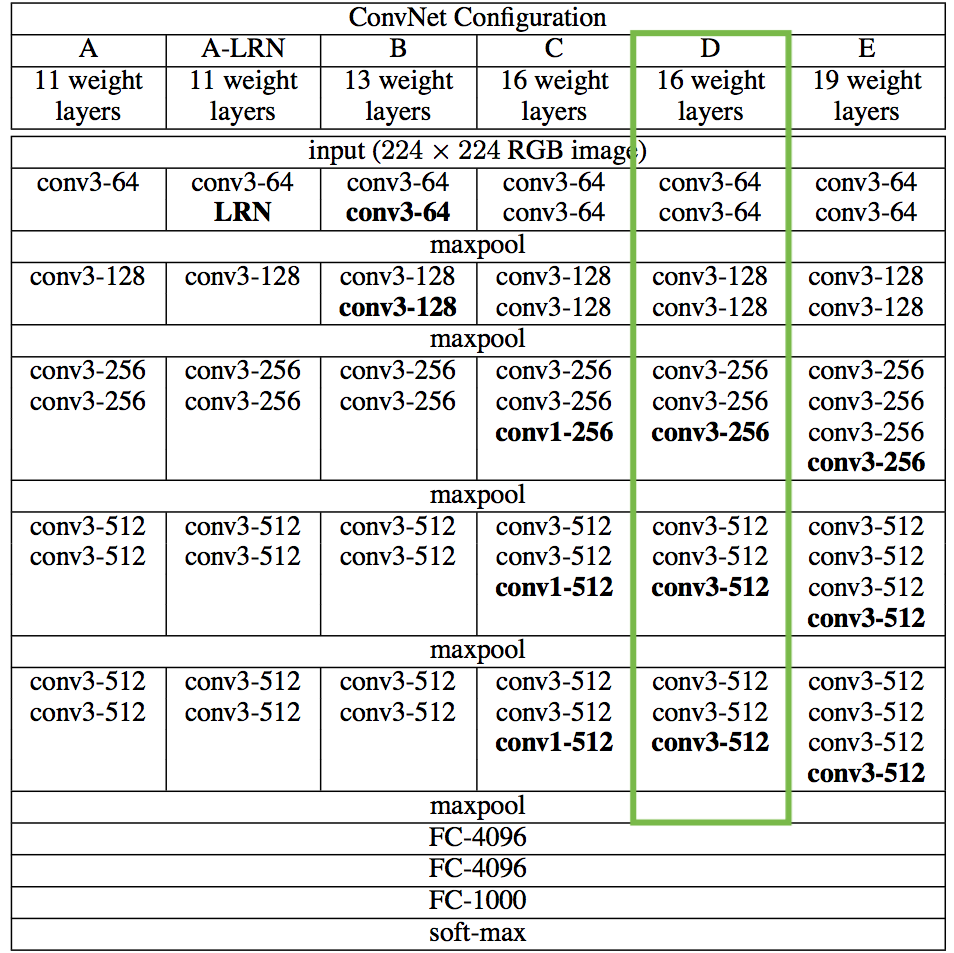
对于我们来说,访问这个被截尾模型是很简单的,因为Keras提供了一组预先训练的模型,包括我们感兴趣的VGG16模型。注意,通过在下面的代码中设置“include_top=False”,我们不包括任何完全连接的层。
model = VGG16(input_tensor=input_tensor, weights='imagenet',
include_top=False)
从上面的表格中可以清楚地看到,我们所使用的模型有很多层。Keras对这些层有自己的名字。让我们列出这些名称的列表,以便以后可以方便地引用各个层。
layers = dict([(layer.name, layer.output) for layer in model.layers])
layers
out[4]:
{'block1_conv1': <tf.Tensor 'block1_conv1_3/Relu:0' shape=(3, 512, 512, 64) dtype=float32>,
'block1_conv2': <tf.Tensor 'block1_conv2_3/Relu:0' shape=(3, 512, 512, 64) dtype=float32>,
'block1_pool': <tf.Tensor 'block1_pool_3/MaxPool:0' shape=(3, 256, 256, 64) dtype=float32>,
'block2_conv1': <tf.Tensor 'block2_conv1_3/Relu:0' shape=(3, 256, 256, 128) dtype=float32>,
'block2_conv2': <tf.Tensor 'block2_conv2_3/Relu:0' shape=(3, 256, 256, 128) dtype=float32>,
'block2_pool': <tf.Tensor 'block2_pool_3/MaxPool:0' shape=(3, 128, 128, 128) dtype=float32>,
'block3_conv1': <tf.Tensor 'block3_conv1_3/Relu:0' shape=(3, 128, 128, 256) dtype=float32>,
'block3_conv2': <tf.Tensor 'block3_conv2_3/Relu:0' shape=(3, 128, 128, 256) dtype=float32>,
'block3_conv3': <tf.Tensor 'block3_conv3_3/Relu:0' shape=(3, 128, 128, 256) dtype=float32>,
'block3_pool': <tf.Tensor 'block3_pool_3/MaxPool:0' shape=(3, 64, 64, 256) dtype=float32>,
'block4_conv1': <tf.Tensor 'block4_conv1_3/Relu:0' shape=(3, 64, 64, 512) dtype=float32>,
'block4_conv2': <tf.Tensor 'block4_conv2_3/Relu:0' shape=(3, 64, 64, 512) dtype=float32>,
'block4_conv3': <tf.Tensor 'block4_conv3_3/Relu:0' shape=(3, 64, 64, 512) dtype=float32>,
'block4_pool': <tf.Tensor 'block4_pool_3/MaxPool:0' shape=(3, 32, 32, 512) dtype=float32>,
'block5_conv1': <tf.Tensor 'block5_conv1_3/Relu:0' shape=(3, 32, 32, 512) dtype=float32>,
'block5_conv2': <tf.Tensor 'block5_conv2_3/Relu:0' shape=(3, 32, 32, 512) dtype=float32>,
'block5_conv3': <tf.Tensor 'block5_conv3_3/Relu:0' shape=(3, 32, 32, 512) dtype=float32>,
'block5_pool': <tf.Tensor 'block5_pool_3/MaxPool:0' shape=(3, 16, 16, 512) dtype=float32>,
'input_2': <tf.Tensor 'concat_1:0' shape=(3, 512, 512, 3) dtype=float32>}
损失函数
我参考的论文的关键在于,风格转移问题可以作为一个优化问题解决,我们想要最小化的损失函数可以分解为三个不同的部分:内容损失、风格损失和总变化损失。
这些项的相对重要性由一组标量权重确定。这些都是任意的,但是在经过了相当多的实验之后,我们选择了下面的数值,以找到一个能够生成令我满意的输出。
content_weight = 0.025
style_weight = 5.0
total_variation_weight = 1.0
现在,我们将使用模型的特定层提供的特性空间来定义这三个损失函数。我们首先将总的损失初始化为0,并逐步增加。
loss = backend.variable(0.)
内容损失
大体来说,内容丢失是内容和组合图像特征表示之间的(缩放、平方)欧几里得距离。
def content_loss(content, combination):
return backend.sum(backend.square(combination - content))
layer_features = layers['block2_conv2']
content_image_features = layer_features[0, :, :, :]
combination_features = layer_features[2, :, :, :]
loss += content_weight * content_loss(content_image_features,
combination_features)
样式损失
这里开始就比较复杂了,需要用到一个叫Gram矩阵的东西。(详细课参考这篇文章)通过适当地重塑特征空间,并利用外积,可以有效地计算出Gram矩阵。
def gram_matrix(x):
features = backend.batch_flatten(backend.permute_dimensions(x, (2, 0, 1)))
gram = backend.dot(features, backend.transpose(features))
return gram
def style_loss(style, combination):
S = gram_matrix(style)
C = gram_matrix(combination)
channels = 3
size = height * width
return backend.sum(backend.square(S - C)) / (4. * (channels ** 2) * (size ** 2))
feature_layers = ['block1_conv2', 'block2_conv2',
'block3_conv3', 'block4_conv3',
'block5_conv3']
for layer_name in feature_layers:
layer_features = layers[layer_name]
style_features = layer_features[1, :, :, :]
combination_features = layer_features[2, :, :, :]
sl = style_loss(style_features, combination_features)
loss += (style_weight / len(feature_layers)) * sl
总变化损失
总变化损失,total variation loss(a regularisation term) that encourages spatial smoothness.
def total_variation_loss(x):
a = backend.square(x[:, :height-1, :width-1, :] - x[:, 1:, :width-1, :])
b = backend.square(x[:, :height-1, :width-1, :] - x[:, :height-1, 1:, :])
return backend.sum(backend.pow(a + b, 1.25))
loss += total_variation_weight * total_variation_loss(combination_image)
优化问题
这里的目标是解决一个最优化问题。现在我们有了我们的输入图像和我们的损失函数的计算方法,我们剩下要做的就是定义相对于组合图像的总损失的梯度,并使用这些梯度来迭代地改进我们的组合图像以最小化损失。
从梯度的定义开始。
grads = backend.gradients(loss, combination_image)
然后,我们引入了一个Evaluator类,通过两个独立的函数,loss和grads,在一个过程中计算损失和梯度。这是因为scipy.optimize需要分离损失和梯度的功能,但是单独计算它们将是低效的。
outputs = [loss]
outputs += grads
f_outputs = backend.function([combination_image], outputs)
def eval_loss_and_grads(x):
x = x.reshape((1, height, width, 3))
outs = f_outputs([x])
loss_value = outs[0]
grad_values = outs[1].flatten().astype('float64')
return loss_value, grad_values
class Evaluator(object):
def __init__(self):
self.loss_value = None
self.grads_values = None
def loss(self, x):
assert self.loss_value is None
loss_value, grad_values = eval_loss_and_grads(x)
self.loss_value = loss_value
self.grad_values = grad_values
return self.loss_value
def grads(self, x):
assert self.loss_value is not None
grad_values = np.copy(self.grad_values)
self.loss_value = None
self.grad_values = None
return grad_values
evaluator = Evaluator()
现在我们终于可以解决我们的优化问题了。这种组合图像开始作为一个随机的(有效)像素的集合,我们用L-BFGS算法(拟牛顿算法的比标准梯度下降)更快地收敛迭代改进。
我们在10次迭代后停止,因为输出看起来对我很好,并且损失不再显著减少。训练的过程是非常耗时的,因为每次我们想要生成图像时,我们都在求解一个完整的优化问题。(我的小破笔记本迭代一次大概要1000s)
x = np.random.uniform(0, 255, (1, height, width, 3)) - 128.
iterations = 10
for i in range(iterations):
print('Start of iteration', i)
start_time = time.time()
x, min_val, info = fmin_l_bfgs_b(evaluator.loss, x.flatten(),
fprime=evaluator.grads, maxfun=20)
print('Current loss value:', min_val)
end_time = time.time()
print('Iteration %d completed in %ds' % (i, end_time - start_time))
out[5]:
Start of iteration 0
Current loss value: 1.19163e+11
Iteration 0 completed in 994s
Start of iteration 1
Current loss value: 7.60726e+10
Iteration 1 completed in 965s
Start of iteration 2
Current loss value: 6.61486e+10
Iteration 2 completed in 993s
...
结果展示
x = x.reshape((height, width, 3))
x = x[:, :, ::-1]
x[:, :, 0] += 103.939
x[:, :, 1] += 116.779
x[:, :, 2] += 123.68
x = np.clip(x, 0, 255).astype('uint8')
Image.fromarray(x)
out[6]: 
采用不同的样式图片有产生不同的融合效果: 